写在前面

树是计算机科学中经常用到的一种数据结构，树是一种非线性的数据结构，以分层的方式存储数据。树被用来存储具有层级关系的数据，比如文件系统中的文件；树还被用来存储有序列表。今天，我们来谈一谈一种特殊的树：二叉树。为什么选择二叉树，因为在二叉树上查找非常快，为二叉树添加或删除元素也非常快（而对数组执行添加和删除操作则不是这样）。

树的定义

树是一种非线性的数据结构。要理解树的概念及其术语的含义，用一个例子说明是最好的办法。如下图所示就是一棵树，它是若干结点（A、B、C等都是结点）的集合，是由唯一的根（结点A）和若干互不相交的子树（如B、E、F这3个结点组成的树就是一颗子树）组成的。其中每一颗子树又是一棵树，也是由唯一的根结点和若干棵互不相交的子树组成的。由此可知，树的定义是递归 的，即在树的的一种又用到了树的定义。要注意的是，树的结点数目可以为0，当为0时，这棵树为一颗空树，不存在任何结点，这是一种极其特殊的情况。

树的基本术语

以下皆以上图为例

结点：图中A,B,C等都是结点，结点不仅包含数据元素，而且包含指向子树的分支。例如，A结点不仅包含数据元素A，而且包含3个指向子树的指针。

结点的度：结点拥有的子树个数或者分支的个数。例如，A结点有三棵子树，所以A结点的度为3。

树的度：树中各结点度的最大值。例如，上图中这棵树的度就为3，因为所有的结点中，以A结点拥有的子树最多，所以整棵树的度就取A结点的度，即为3。

叶子结点：又叫作终端结点，指的是没有子结点的结点，也可以说度为0的结点，例如，E,F,G都时叶子结点。

非终端结点：又叫作分支结点，指度不为0的结点，如A,B,C,D结点都是非终端结点，除了根结点之外的非终端结点，也叫作内部结点，如B,C,D都是内部结点。

孩子：结点的子树的根。如A结点的孩子为B,C,D。

双亲：与孩子的定义对应，如B,C,D的结点的双亲都是A。

兄弟：同一个双亲的孩子之间互称为兄弟。如B,C,D互为兄弟，因为它们都是A结点的孩子。

祖先：从根到某结点的路径上的所有结点，都是这个结点的祖先。如F结点的祖先为A和B，因为从A到F的路径为A-B-F。

子孙：以某结点为根的子树中的所有结点，都是这个结点的子孙。如B结点的子孙为E,F。

层次：从根开始，根为第一层，根的孩子为第二层，根的孩子的孩子为第三层，以此类推。

树的高度（或者深度）：树中结点的最大层次。如上例中的树共有3层，所以深度为3。

结点的深度或高度：结点深度是从根结点算起的，根结点的深度为1；结点高度是从最底层的叶子结点算起的，最底层叶子结点的高度为1。

堂兄弟：双亲在同一层的结点互为堂兄弟。如F和G互为堂兄弟，因为G的双亲为D，F结点的双亲为B，而B和D在同一层上。注意堂兄弟和兄弟之分。

有序树：树中结点的子树从左到右是有次序的，不能交换，这样的树叫作有序树。

无序树：树中结点的子树没有顺序，可以任意交换，这样的树叫作无序树。

丰满树：丰满树即理想平衡树，要求除最底层外其他层都是满的。

森林：若干棵互不相交的树的集合。例子中如果把根A去掉，剩下的3棵子树互不相交，它们组成一个森林。

二叉树的定义

在理解了树的定义之后，二叉树的定义也就很好理解了。将一般的树加上两个限制条件就可以得到二叉树：

（1）每个结点最多只有两棵子树，即二叉树中结点的度只能为0，1，2；

（2）子树有左右之分，不能颠倒；

二叉树的主要性质

性质1：非空二叉树上叶子结点数等于双分支节点数加1；

性质2：二叉树的第 k 层上最多有(k >= 1)个结点；

性质3：高度（或深度）为 k 的二叉树最多有（k >= 1）个结点。换句话说，满二叉树前 k 层的结点个数为；

性质4： 有 n 个结点的完全二叉树，对各结点从上到下，从左到右依次编号（编号范围为 1 ~ n），则结点之间有如下关系：

若 k 为某个结点 a 的编号，则：

如果 k ≠ 1，则 a 的双亲结点的编号为 ；

如果 2k ≤ n，则 a 结点的左孩子的编号为 2k；

如果 2k > n，则 a 结点无左孩子；

如果 2k + 1 ≤ n，则 a 结点的右孩子的编号为 2k + 1；

如果 2k + 1 > n，则 a 结点无右孩子。

性质5：Catalan函数：给定 n 个结点，能构成h(n)种不同的二叉树，h(n) = ；

性质6：具有 n 个结点的完全二叉树的高度（或深度）为  或者 .

使用Javascript实现二叉查找树

二叉查找树是一种特殊的二叉树，相对较小的值保存在左结点中，较大的值保存在右结点中。正是这一特性使得其查找效率很高，对于数值型和非数值型的数据，比如单词和字符串，都是如此。

由于个人喜好，以下代码皆以typescript来进行，用JS亦可。

二叉查找树由结点组成，我们先定义一个用来实现二叉查找树中的结点的类，简单的分析，可以知道，每个结点都有左右结点，所以，我们不妨为此类添加实例属性left和right，用来保存其左右结点，初始化都为null，再添加一个实例属性data用来保存结点数据。代码如下：

1
2
3
4
5
6
7
8
9
10
class BinaryNode {
  data: number | string
  left: BinaryNode
  right: BinaryNode
  constructor(data: number | string) {
    this.data = data
    this.left = null
    this.right = null
  }
}

如此，结点依然准备完毕，接下来我们就来创建二叉查找树的类，简单的分析，首先每棵树都有一个根结点，所以我们为二叉查找树的类添加一个实例属性root用来保存此树的根结点，根结点初始化为null：

1
2
3
4
5
6
class BinaryTree {
  root: BinaryNode
  constructor() {
    this.root = null
  }
}

接下来，我们要为树添加一个方法用来插入数据节点，我们知道，在二叉查找树中，较小的值分布在左子树，较大的值分布在右子树；较小的值放在左结点，较大的值放在右结点；那么，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
insert(data: number | string): void {
    if (this.root == null) {
      this.root = new BinaryNode(data)
    } else this.insertNode(this.root, data)
  }

  private insertNode(node: BinaryNode, data: string | number): void {
    if (data < node.data) {
      if (node.left == null) {
        node.left = new BinaryNode(data)
      } else this.insertNode(node.left, data)
    } else {
      if (node.right == null) {
        node.right = new BinaryNode(data)
      } else this.insertNode(node.right, data)
    }
  }

这里声明了两个方法用来实现插入数据操作，insert方法用来进行插入数据，insertNode实现具体的插入过程，可以看到，插入数据的过程其实是递归的进行比较的过程（因insertNode方法没必要对外包暴漏，所以这里进行了私有化）。

那么，我们简单的插入一组数据试试看：

1
2
3
4
5
6
7
8
9
10
11
let tree: BinaryTree = new BinaryTree

tree.insert(23)
tree.insert(45)
tree.insert(16)
tree.insert(37)
tree.insert(3)
tree.insert(99)
tree.insert(22)

console.log(tree)

输入如下：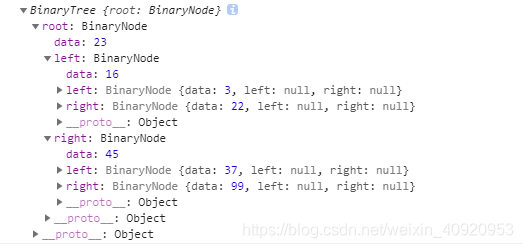

可以很明显的看到，二叉查找树已经按照预期实现了，数据插入也符合预期，较大的值在右子树上，较小的值在左子树上；较小的值在左结点上，较大值在右结点上。

二叉查找树的遍历

1. 中序遍历

中序遍历按照结点上的键值，以升序访问树上的所有结点，先访问左子树，再访问根结点，后访问右子树。代码如下：

1
2
3
4
5
6
7
inOrder(node: BinaryNode): void {
    if (node !== null) {
      this.inOrder(node.left)
      console.log(node.data)
      this.inOrder(node.right)
    }
  }

这里我们值是简单的将结点的值打印在控制台中，你完全可以选择进行其他的操作。我们调用一下中序遍历的方法，如下：

tree.inOrder(tree.root)

发现控制台输出如下：

很明显的发现，结点数据会以升序的方式进行排序。

2. 先序遍历

由上述，我们知道中序遍历可以对树上的节点数据进行升序排序，那么先序遍历的意义是什么呢？先序遍历对一棵二叉树进行复制，要知道复制一颗二叉树的效率要比重新创建一棵二叉树高得多，复制一棵二叉树的算法复杂度为O(n)，而新创建一棵二叉树的算法复杂度为O(nlogn)，所以这就是研究先序遍历的意义。先序遍历先访问根结点，再访问左子树，最后访问右子树。

1
2
3
4
5
6
7
preOrder(node: BinaryNode): void {
    if (node !== null) {
      console.log(node.data)
      this.preOrder(node.left)
      this.preOrder(node.right)
    }
  }

那么，我们也不妨调用一下看看：

tree.preOrder(tree.root)

输出如下：

3. 后序遍历

后序遍历，先访问左子树，在访问右子树，最后访问根结点。代码如下：

1
2
3
4
5
6
7
postOrder(node: BinaryNode): void {
    if (node !== null) {
      this.postOrder(node.left)
      this.postOrder(node.right)
      console.log(node.data)
    }
  }

调用一下：

tree.postOrder(tree.root)

输出如下：

查找结点

那么，在二叉查找树怎么找到某一个数据的结点呢？我们提供了一个查找数据结点的方法：

1
2
3
4
5
6
7
8
9
10
findNode(node: BinaryNode, data: string | number): BinaryNode {
    if (node === null) {
      return null
    }
    if (node.data === data) {
      return node
    } else if (node.data > data) {
      return this.findNode(node.left, data)
    } else return this.findNode(node.right, data)
  }

调用一下看看：

1
2
console.log(tree.findNode(tree.root, 37));
console.log(tree.findNode(tree.root, 137));

输出如下：

很明显，第二个结点并不存在于此树中，所以返回了null。

查找最大值和最小值结点

我们知道，二叉查找树中，较小的值分布再左子树，较大的树分布在右子树，所以，这也为我们寻找最大值和最小值结点提供了思路，方法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
   * 获取最小值节点
   *
   * @param {BinaryNode} node
   * @returns
   * @memberof BinaryTree
   */
  getMinNode(node: BinaryNode): BinaryNode {
    if (node !== null) {
      while (node && node.left !== null) {
        node = node.left
      }
      return node
    }
    return null
  }

  /**
   * 获取二叉树最大值节点
   *
   * @param {BinaryNode} node
   * @returns
   * @memberof BinaryTree
   */
  getMaxNode(node: BinaryNode): BinaryNode {
    if (node !== null) {
      while (node && node.right !== null) {
        node = node.right
      }
      return node
    }
    return null
  }

不妨来实验一下，调用一下：

1
2
console.log(tree.getMinNode(tree.root));
console.log(tree.getMaxNode(tree.root));

输出如下：

其实，这两个方法也可以用来查找子树的最大值和最小值：

1
2
3
let node = tree.findNode(tree.root, 45)
console.log(tree.getMinNode(node))
console.log(tree.getMaxNode(node))

输出如下：

可以发现，也如预期的找出了子树中的最大值和最小值。

删除结点

重头戏来了，二叉查找树最复杂的部分就是删除某个结点的操作，其复杂程度取决于删除哪个结点。如果删除没有子结点的结点，那么非常简单。如果结点只有一个子结点，不管是左结点还是右结点，就变得稍微有点复杂了。删除包含两个子结点的结点最复杂。

简单的分析一下先，如果删除的是叶子结点（没有子结点的结点），那么只需要将只需将原本指向它的父结点指向的链接指向null即可；如果删除的结点只包含一个子结点，那么原本指向它的结点就得做些调整，使其指向它的子结点；最后，如果待删除的结点包含两个子结点，正确的做法有两种：要么查找待删除结点的左子树上的最大值，要么查找待删除结点右子树上的最小值。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
remove(data: number | string): void {
    this.root = this.removeNode(this.root, data)
  }

  private removeNode(node: BinaryNode, data: number | string): BinaryNode {
    if (node == null) {
      return null
    }
    if (data < node.data) {
      node.left = this.removeNode(node.left, data)
      return node
    } else if (data > node.data) {
      node.right = this.removeNode(node.right, data)
      return node
    } else {
      if (node.left === null && node.right === null) {
        return null
      }
      if (node.left === null) {
        return node.right
      }
      if (node.right === null) {
        return node.left
      }
      let tempNode = this.getMinNode(node.right)
      node.data = tempNode.data
      node.right = this.removeNode(node.right, tempNode.data)
      return node
    }
  }